#数楽 複素函数のグラフをどう描くは面白い問題。2次元平面領域から2次元平面への写像なので、グラフは4次元空間内の2次元の曲面になる。私はベクトル場とみなしてプロットしてみることがよくある。実例に続く。https://twitter.com/croce1/status/854172515438022656 …

#数楽 添付画像は http://www.wolframalpha.com/input/?i=vector field plot (x^3-3xy^2-1,3x^2y-y^3) … より。f(z)=z^3-1に対応するベクトル場の積分曲線。1の3乗根でベクトル場がゼロになっていることがわかる。続くpic.twitter.com/13pw8wihB9
#数楽 一般に複素函数f(z)に対して、u=Re f(z), v=Im f(z) とおくとき、ベクトル場 (u,-v) をプロットするとよい。虚部を-1倍しておくと、コーシー・リーマンの方程式から湧き出しと渦無しの流れになる。湧き出しや渦は極に現われる。続く
#数楽 scilab で描いた複素函数のベクトル場の例は以下のまとめにある。 "scilabによるプロット:ベクトル場とKdV方程式" 作成者:
@genkurokihttps://twitter.com/i/moments/850348029961846785 …
#数楽 すみません。リンク先の添付画像が f(z)=z^3-1 のベクトル場のプロットだいうのは誤りです。次のツイートで訂正版を出します。https://twitter.com/genkuroki/status/854695909254283264 …
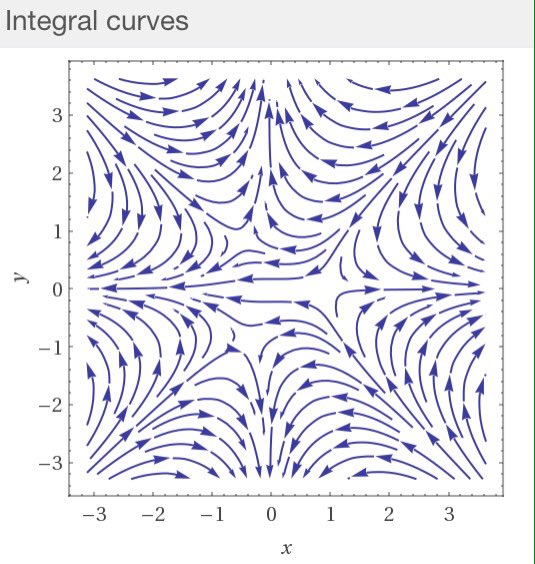
#数楽 訂正版。(x+iy)^3-1=(x^3-3xy^2-1)-i(y^3-3xy^2) のベクトル場のプロット。1の3乗根でベクトル場は0になっている。http://www.wolframalpha.com/input/?i=vector field plot (x^3-3xy^2-1,y^3-3x^2y) …pic.twitter.com/ZQTvtm4Hyp
#数楽 それでは、リンク先のプロットの方にも1の3乗根の場所がくっきり現われているのは偶然か?偶然ではない。続くhttps://twitter.com/genkuroki/status/854695909254283264 …
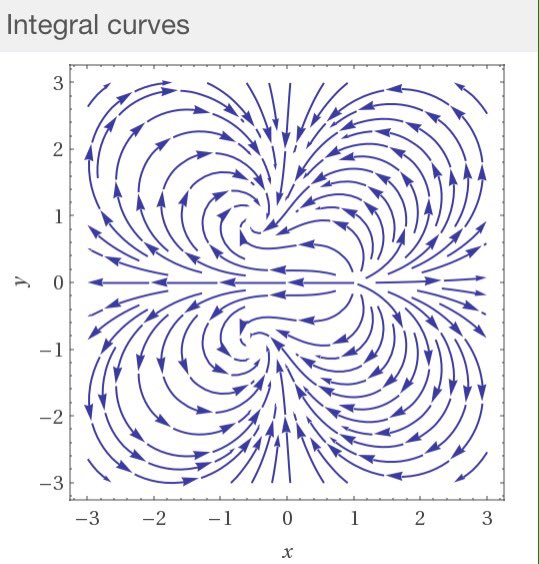
#数楽 続き。誤りとしたベクトル場は1/(z^3-1)の「分母」をのぞいた分のベクトル場である。1/(z^3-1)のベクトル場(の積分曲線)のプロットは添付画像の通り。http://www.wolframalpha.com/input/?i=vector field plot (x^3-3xy^2-1,-y^3+3x^2y)/((x^3-3xy^2-1)^2+(-y^3+3x^2y)^2), -3
#数楽 1/(z^3-1)の極はz=1,e^{±2πi/3}にあり、それぞれ留数は1/3,-1/6±i√3/6です。z=1から流れ出した1/3の電気力線がz=e^{±2πi/3}に1/6ずつ流れ込んでいる。z=e^{±2πi/3}での渦度は±√3/6で回転の向きは逆。
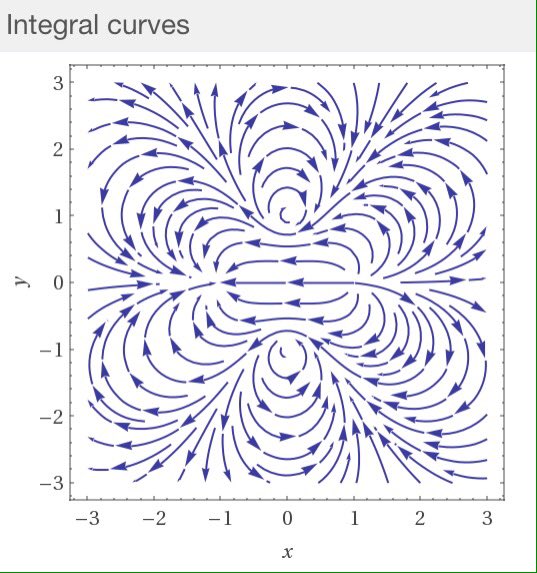
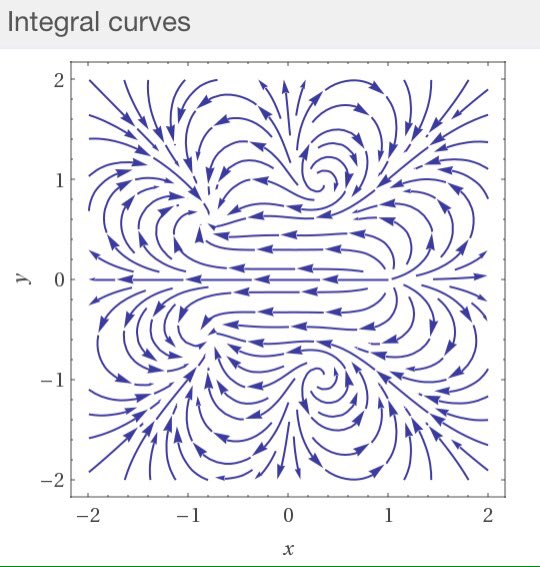
#数楽 1/(z^4-1)のベクトル場。z=±1が湧き出しと吸い込み、z=±iが互いに逆回転の渦。http://www.wolframalpha.com/input/?i=vector field plot (Re(1/((x+iy)^4-1)),-Im(1/((x+iy)^4-1))), -3
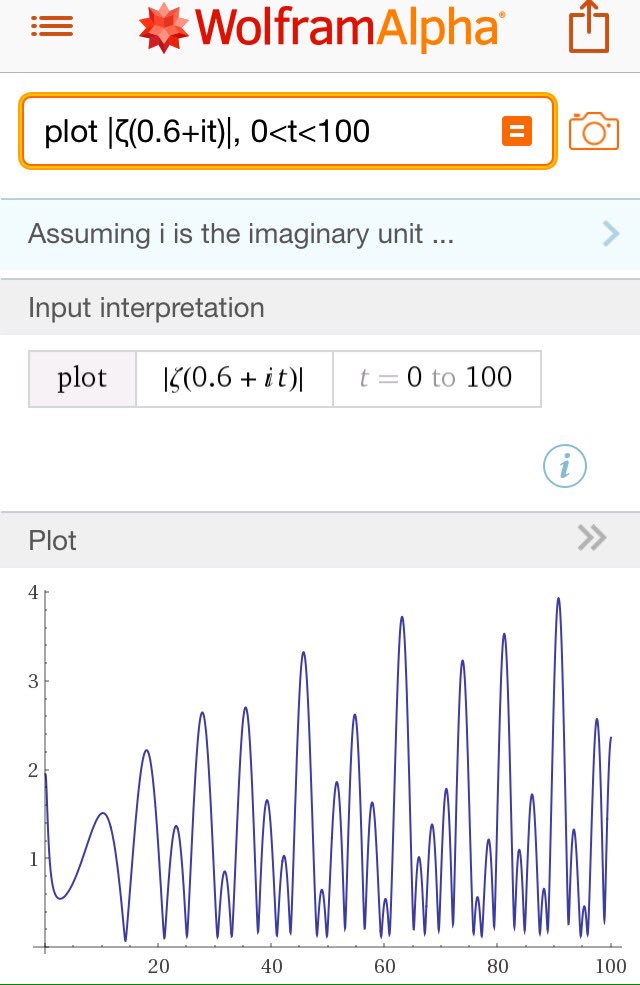
#数楽 ついでに |ζ(0.6+it)| のプロット。さすがに零点らしきところは見つからない(笑)。http://www.wolframalpha.com/input/?i=plot%20|ζ(0.6+it)|, 0
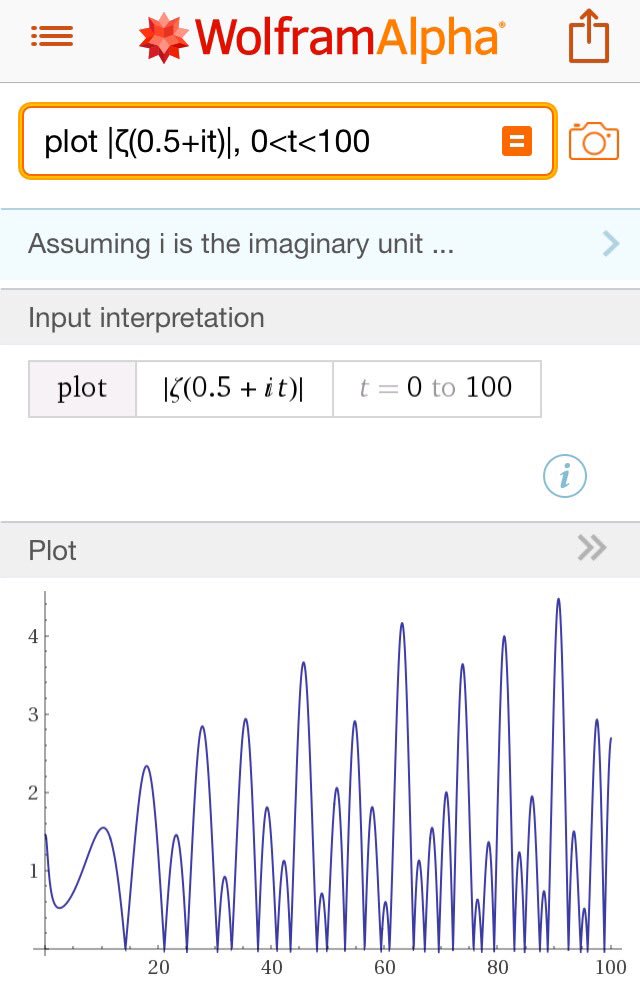
#数楽 数学好きの少年にとって、リーマンのゼータ函数の零点の様子を寝床で寝転んで見て楽しむことは夢の一つだったと思うのですが、このように実現してしまっている。



